Reformer 뽀개기 (저리가! Transformer) Part 2

Reversible Residual Network

Reversible Redisual Network는 결론적으로 memory 크기에 효율성을 가져오기 위해 도입된다.

그럼 도입되기 전후로 Transformer / Reformer를 비교해보자.

Transformer

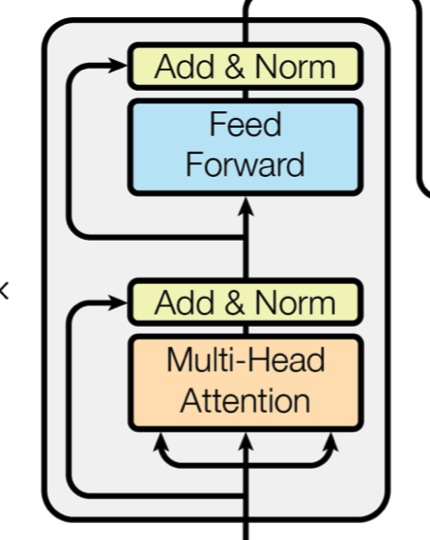
Page 6

Even worse: inside the feed-forward layers of Transformer this goes up to b · l · dff · nl. In a big Transformer it is usual to set dff = 4K and nl = 16 so with l = 64K this again would use an impractical 16GB of memory

Transformer에서 다른 parameter가 모두 동일하다고 가정하고 Deep한 모델을 만들기 위하여 layer의 개수를 늘린다고 해보자. 결국 파라미터는 nl의 비례하여 커지고, 만약 Big-Transformer로 설계한 경우 dff(4000) * nl(16) * l(64000) * 4(float32) = 16GB 메모리 크기가 16GB가 된다.

Reformer

Reformer의 경우 Reversible Residual Network를 도입하여 nl에 대한 memory cost를 무시하게 된다.

Reversible Residual Network의 아이디어는 간단하다.

만약 어떤 activations에 대하여 backpropagation을 계산한다면, 거꾸로(Reversible) 계산하면 된다는 이야기다.

Y1이 X1 + Attention(X2)라고 하고, Y2 = X2 + FeedForward(Y1)이라고 해보자.

결국 backpropagation을 위해서 계산해야 할 것은 X2 = Y2 - FeedForward(Y1) , X1 = Y1 - Attention(X2) 위와 같이 역으로 계산하기만 하면 된다. 또잉? 너무 쉬워서 처음에 너무 당혹스러울 것이다. 미분이고 뭐고 필요없고, backprogapation을 직접 정의하여 계산하면 되는거다.

//https://github.com/Debian/tensorflow/blob/master/tensorflow/contrib/eager/python/examples/revnet/blocks.py
  
with tf.GradientTape(persistent=True) as tape:
      y = tf.identity(y)
      tape.watch(y)
      y1, y2 = tf.split(y, num_or_size_splits=2, axis=self.axis)
      z1 = y1
      gz1 = self.g(z1, training=training)
      x2 = y2 - gz1
      fx2 = self.f(x2, training=training)
      x1 = z1 - fx2

기존에 forward 혹은 call만 정의하면 가능한 layer 혹은 model에 대해서 대신 직접 정의해야 한다는 단점이 있다.

위 부분은 모든 memory에 대한 차지를 무시하는 것이 아니라 nl에 대한 term만 무시하게끔 설계되는데,

결국 nl만큼 attention과 feedforward는 반복된다고 할 때, nl만큼 반복되더라도 거꾸로 계산된 것을 backpropgation의 input으로 받아, 이전 Layer에 대한 backpropagation을 계산하고, … 위 작업이 반복되면 결국 반복되는 reversible layer에 대한 memory 차지를 고려할 필요가 없게 된다.

그러나, 그만큼 연산량은 늘어나게 된다.

먼저 기존 backpropagation의 경우 N개의 connection을 가진다고 가정했을 때 forward 연산에서 N, backpropagation에서 gradient 계산과 update까지 들어가 2N이 되어 총 3N의 연산량이 필요하다.

그러나, reversible residual network의 경우 backward 부분에서 forward연산에 사용했던 residual function을 다시 계산해야 하므로, N만큼의 연산량이 추가되어 3N + N 즉, 4N만큼의 연산량이 필요하다.

그러면 Reversible 구조에서 모든 함수가 residual function으로 사용가능할까? 당연히 아니다.

Reversible Residual Network Page 4

In general, a practical architecture would likely also include non-reversible layers, such as subsampling layers; the inputs to these layers would need to be stored explicitly during backprop.

원본 데이터가 복구될 수 없는 (환원할 수 없는) function의 경우 reversible residual network에서 사용할 수 없다.

Page 6

Chunking. While reversibility covers the nl term, the thicker layers can still use a lot of memory. The feed-forward layer in particular can use intermediate vectors of dimensionality dff = 4K or higher. However, computations in feed-forward layers are completely independent across positions in a sequence, so the computation can be split into c chunks

feed-forward network 부분에서 chunking을 통해 memory에 대한 효율성을 갖게 된다.

결국 가능한 것은 inpute들이 서로 position에 대해서 영향을 끼치는 요소가 없기 때문에, c개만큼으로 chunk한다는 것이다.