Reformer 뽀개기 (저리가! Transformer)

(제목에 어그로를 이해해주시기 바랍니다.. 트랜스포머 만세!)

Reformer를 이해하기까지의 여정이 잘 표현된 것 같다… ( 도착은 했겠지..?)

논문리뷰 스터디에서 자연어처리 팀장이 되면서 제일 먼저 추진한 논문이다.

처음 읽었을 때도 상당히 어려웠었는데, 발표 준비를 위해 다시 읽어보는데 더 어려운 것 같다.

리포머의 경우 Locality Sensitive Hashing, Reversible Residual Network와 같은 어려운 개념들이 많이 등장해서 이 논문만은 line by line으로 설명을 하는 게 어떨까 한다.

리포머의 등장배경

현재 자연어처리의 경향이 어떻냐고 물어본다면 당연 Bert의 시대라고 답할 수 있을 것이다.

Transformer 모델에 대한 연구가 많이 이뤄지고, 2019년 동안은 Bert 대한 연구가 이루어졌다.

그러나, Big Transformer 모델의 경우 큰 Enterprise에서는 사용가능 하나 새로 시작하는 스타트업 및 GPU가 적은 환경에서 이용하기 힘들다. 물론, Distillation과 Compress 방법을 통해서 모델의 크기를 줄여나갈 수 있지만, Big 모델을 사전적으로 학습을 해야한다는 문제가 있다.

리포머의 성능

먼저, 흥미를 끌기 위하여 리포머의 성능에 대해서 이야기하고 싶다.

page 2

• Reversible layers, first introduced in Gomez et al. (2017), enable storing only a single copy

of activations in the whole model, so the N factor disappears.

Reversidual Residual Network를 이용하여 Transformer의 layer에 대한 memory 저장을 필요없게 한다.

즉, backpropagation에서 메모리 효율성을 가져올 수 있다.

• Splitting activations inside feed-forward layers and processing them in chunks removes the

dff factor and saves memory inside feed-forward layers.

feed-forward 연산을 한꺼번에 하기보다 연산과정을 chunking 함으로써 chunking하는 부분만큼만 Memory에 올릴 수 있어 메모리 효율성을 가져올 수 있다.

• Approximate attention computation based on locality-sensitive hashing replaces the O(L^2)

factor in attention layers with O(Llog L) and so allows operating on long sequences.

LSH 알고리즘을 이용하여 Attention을 구하는 computing, memory 복잡도를 낮췄다. 여기서 L은 sequence-length다.

Weight sharing

page 3

This is easily achieved by using the same linear layer to go from A to Q and K, and a separate one for V. We call a model that behaves like this a shared-QK Transformer

논문 결과에서 Query의 weight와 Key의 weight를 공유해도 성능에 지장이 없다고 한다.

weight sharing을 함으로써 가져올 수 있는 효과는 ¹

1. 메모리 측면에서 weight에 대한 부분만큼 save

2. 모델을 덜 유연하게 만듦으로써 일종의 regularizer의 역할

   # https://github.com/lucidrains/reformer-pytorch/blob/master/reformer_pytorch/reformer_pytorch.py
   class LSHSelfAttention(nn.Module):
       def __init__(self, dim, heads = 8, bucket_size = 64, n_hashes = 8, causal = False, attn_chunks = 1, random_rotations_per_head = False, attend_across_buckets = True, allow_duplicate_attention = True, num_mem_kv = 0, one_value_head = False, use_full_attn = False, full_attn_thres = None, return_attn = False, post_attn_dropout = 0., dropout = 0., **kwargs):
           super().__init__()
           assert dim % heads == 0, 'dimensions must be divisible by number of heads'
         self.dim = dim
         self.heads = heads
         self.attn_chunks = default(attn_chunks, 1)
      
         self.v_head_repeats = (heads if one_value_head else 1)
         v_dim = dim // self.v_head_repeats
      
         **self.toqk = nn.Linear(dim, dim, bias = False)**
         self.tov = nn.Linear(dim, v_dim, bias = False)
         self.to_out = nn.Linear(dim, dim)
   

실제 구현부는 이와 같이 되어있다. (trax는 너무 비직관적이어서 pytorch 버전으로…) Query,Key에 대한 weight가 공통의 Linear부분으로 선언된 것을 확인할 수 있다.

Locality sensitive hashing (LSH) Attention

page 2

Let us assume that Q, K and V all have the shape [batch size, length, dmodel]. The main issue is the term QKT , which has the shape [batch size, length, length]. In the experimental section we train a model on sequences of length 64K – in this case, even at batch-size of 1, this is a 64K × 64K matrix, which in 32-bit floats would take 16GB of memory.

Transformer의 연산은 scaled-dot-product하는 부분에서 결정된다.

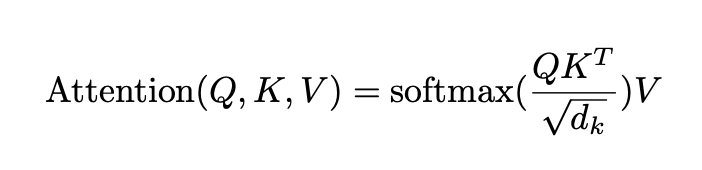
:param q: query # (batch_size, seq_len_q, d_model)
:param k: key # (batch_size, seq_len_k, d_model)
:param v: value # (batch_size, seq_len_v, d_model)
:param mask: mask # (batch_size, num_heads, seq_len_q, seq_len_k)
:return: output of multi-head-attention and attention-weights

Query의 shape가 (batch_size, seq_len_q, d_model), Key의 shape (batch_size, seq_len_k, d_model)라고 하였을 때 복잡도는 O(L^2)가 된다. 또한 이 부분은 메모리를 그만큼 올려야 한다는 것이기 때문에 bottleneck이 된다.

그러면 이 부분을 어떻게 개선할 수 있을까? 힌트는 softmax 부분에서 찾을 수 있다. softmax는 각 vector에 대하여 확률 term으로 나타나고, 이 말은 즉, Attention 과정에서 중요하지 않는 단어들은 무시된다는 것이다.

그렇다면 Attention의 계산에서 각 Query에 대하여 가장 가까운 keys로 Attention을 계산하면 되지 않을까?

위에 대한 부분을 구현한 것이 Locality sensitive hashing (LSH) Attention이다.

LSH 자체에 대해서는 스킵하고자 한다. 위 부분에 대해서 잘 정리한 블로그가 있으니 아래 블로그를 참고하면 좋을 것 같다!

https://towardsdatascience.com/understanding-locality-sensitive-hashing-49f6d1f6134

https://lovit.github.io/machine learning/vector indexing/2018/03/28/lsh/

여기서 LSH 자체에 대한 이해가 어렵지만, 가장 먼저 이해해야 할 것은 Hashing이다.

Hashing이 하고자 하는 것은 어떠한 함수를 통해 어떠한 set(bucket)으로 mapping한다는 것이다.

page 3

We achieve this by employing random projections as follows (see Figure 1). To get b hashes, we first fix a random matrix R of size [dk , b/2]. We then define h(x) = arg max([xR; −xR]) where [u; v] denotes the concatenation of two vectors. This method is a known LSH scheme (Andoni et al., 2015) and is easy to implement and apply to batches of vectors.

LSH에서 결국 하고자 하는 것은 비슷한 것들을 b개의 bucket으로 나누는 것이다. 즉, 데이터들을 hashing을 통해

b개의 bucket으로 projection을 하려고 하는 것이다. 위 과정은 아래와 같이 볼 수 있다.

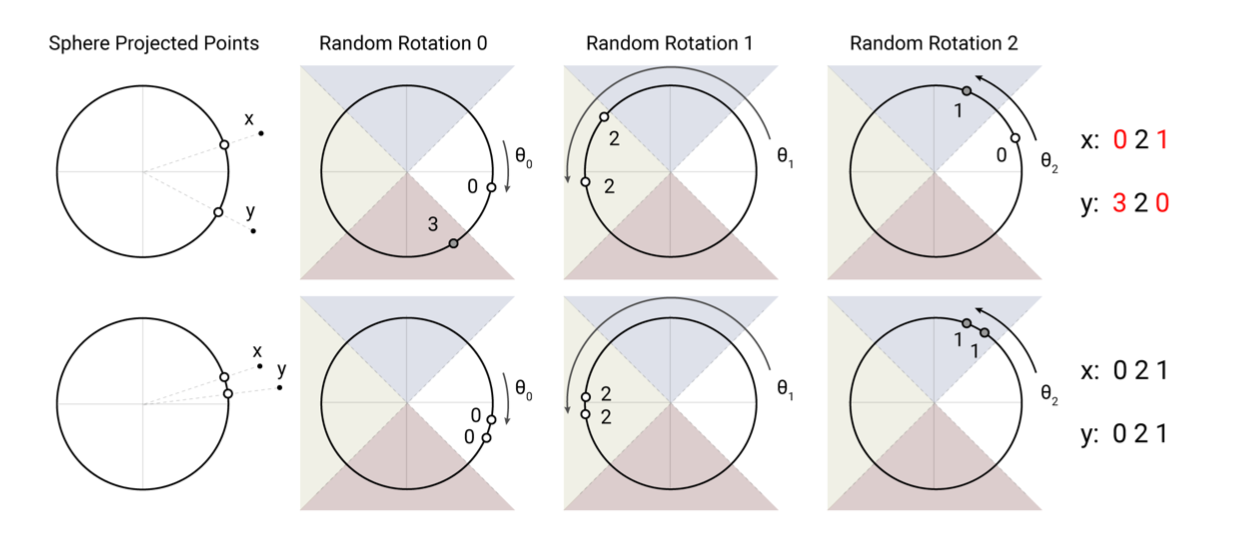
Angular locality sensitive hashing을 이용하게 되는데, 각도를 돌려보아 각 hashing의 결과가 모두 동일하다면

x,y는 비슷하다고 생각할 수 있는 것이다. project matrix를 dot-product를 통해 bucket만큼의 결과를 내보낼 수 있는데, positive sign과 negative sign에 대해서 [xR; −xR] hashing을 하게 된다. hash의 결과가 잘못 매핑될 확률을 조금이라도 더 낮추기 위해서다.

그 다음부터의 설명은 아래의 이미지를 통해 이야기하고자 한다.

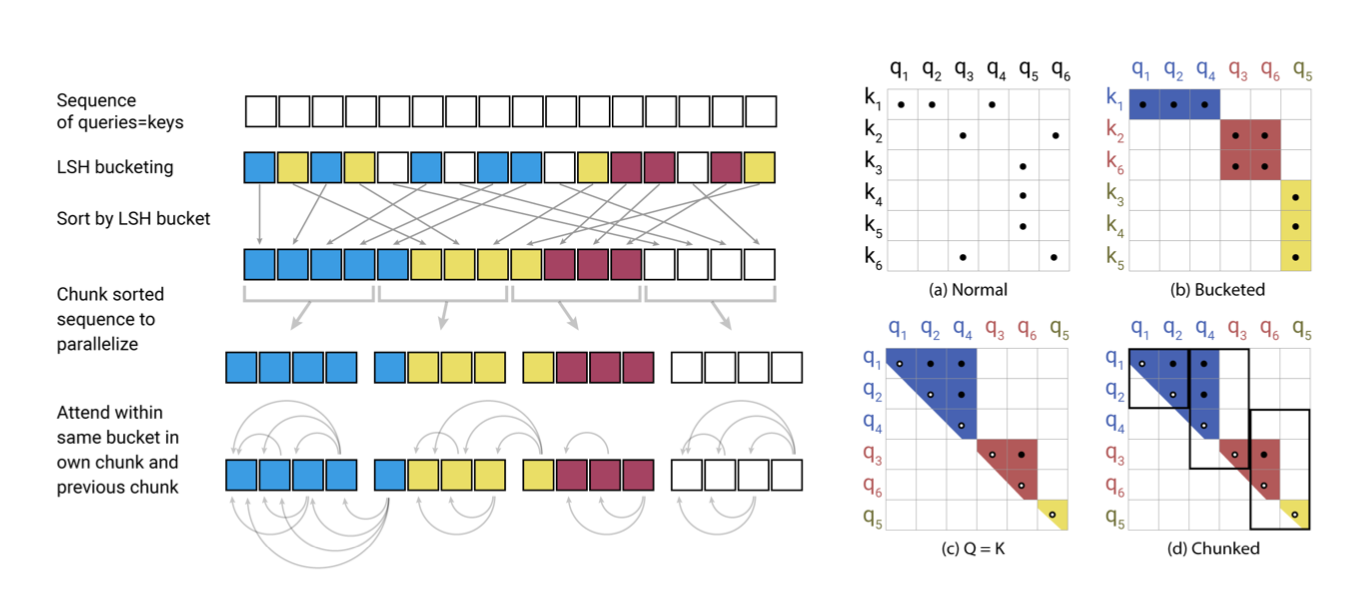
먼저 LSH를 통해 각 bucket으로 mapping한다. 이를 LSH bucketing이라고 한다. 그렇게 되면 각 query에 대응하는 매핑된 key에 대한 집합이 나오게 되는데, 위 부분이

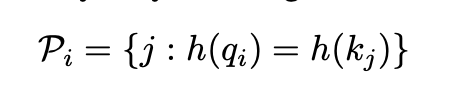
위 파트다. 예를 들어, q1에 대해선 k1, q3에 대해선 k2, k6가 대응된다. 위 결과를 표현한 것이 그림 a다.

page 4

the computation does not take advantage of this sparsity

그러나, 이 작업을 통해서computing에 대해선 장점을 가져올 수 없는데, matrix가 엄청 sparse하기 때문이다.

따라서, bucket의 결과에 따라서 sorting을 해준다. 그러면 위의 그림처럼 딱 그림에서 보여지는 것처럼 나누기가 좋아보인다. (위 부분에 대한 소스는 좋아보이지 않다..)

page 4

Hash buckets in this formulation tend to be uneven in size, which makes it difficult to batch across

buckets. Moreover, the number of queries and the number of keys within a bucket may be unequal –

in fact, it is possible for a bucket to contain many queries but no keys. To alleviate these issues, we

qj first ensure that h(kj ) = h(qj ) by setting kj = qj /∥qj ∥ .

그러나, bucketing 과정에서 어떤 bucket에 결과가 없을 수 있다. 위 그림에서 P3,P6의 j가 2,5만 있다고 해보자.

그러면, k6에 대응하는 것은 없고, key가 없는 bucket이 생겨버린 것이다.

Attention은 Query와 Key에 대해서 scaled-dot-product를 하게 되는데, 계산할 term자체가 사라져버린것이다! (충격!!…)

위 문제를 해결하기 위해 kj = qj/ norm(qj)로 세팅하는 작업을 진행한다. 위에 대한 결과가 그림에서의 c다.

여기서 normalize는 embedding dimension을 축으로 normalize하는 것이다

page 4

그 이후 chunking 작업을 진행한다. 해당 이젠 sorted된 sj에 대하여 chunk_size로 쪼개 집합을 만든다.

우리에게 주어진 그림을 예제로 하자.

m = 2l / n_buckets로 l은 6, n_buckets은 3으로 결국, m=4가 된다.

그리고 평균 bucket size는 m/2로 2가 된다. (reformer 저자는 average bucket size가 2배 이상만큼 될 확률이 상당히 적다고 가정한다) average bucket size만큼 옮겨가면서 m개의 연속되는 쿼리에 대하여 chunking을 할 것인데,만약 Pi의 max index가 m보다 작으면, 그대로 Pi를 chunking한다.

위 그림으로 보면 d에서 q1,q2가 m=4보다 작기 때문에 첫번째 chunking작업만 2개가 되는 것이다.

page 4 & page 5

With hashing, there is always a small probability that similar items nevertheless fall in different buckets

The above task can be solved perfectly (to accuracy 100% and loss 0) by a 1-layer Transformer model. Note though, that it requires non-local attention lookups, so it cannot be solved by any model relying on sparse attention with a limited span. To make it easy and fast to train but similar to models used in NLP, we use a 1-layer Transformer with dmodel = dff = 256 and 4 heads. We train it for 150K steps in 4 different settings: with full attention, LSH attention with nrounds = 1, nrounds = 2 and nrounds = 4.

n_rounds에 대하여 위 부분을 같이 이야기하는 이유는 구현체 때문에 그렇다.

hashing함에도 불구하고 비슷한 데이터가 다른 버킷에 빠질 가능성이 있기 때문에 n_rounds만큼 시도를 한다는 것이다. 그러면 n_rounds만큼 hash 함수가 생기게 된다. 그러나, 아래 테이블에 보는 것과 같이

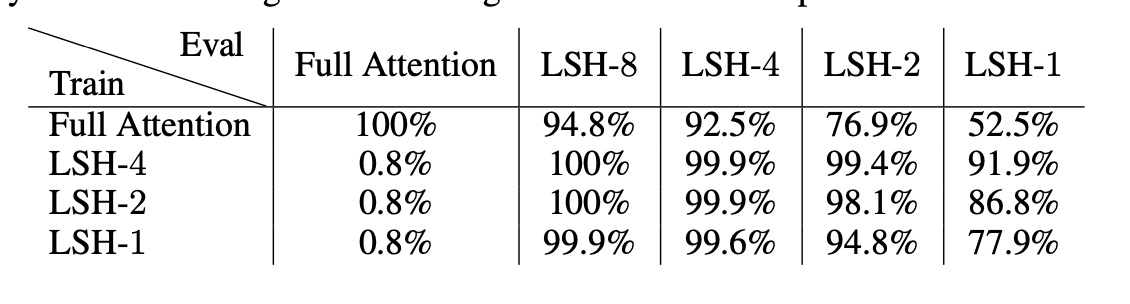
reformer 저자는 train시와 eval시의 n_rounds를 다르게 설정하고 하고있는데, 결구 n_rounds는 모델에 종속적이지 않다는 것이다.

page 5

While attention to the future is not allowed, typical implementations of the Transformer do allow a position to attend to itself. Such behavior is undesirable in a shared-QK formulation because the dot-product of a query vector with itself will almost always be greater than the dot product of a query vector with a vector at another position

쉽게 말해서 query와 key가 같으니 자기참조를 하지 않게 masking을 한다는 것이다.

Reversible Residual Network

위 부분 또한 LSH만큼 중요하므로 Part2에서 정리하도록 하겠다!

coming soon!

Reference